搜索到
4
篇与
的结果
-
![2024年6月上海月赛甲组T3积木染色(五)题解]()
-
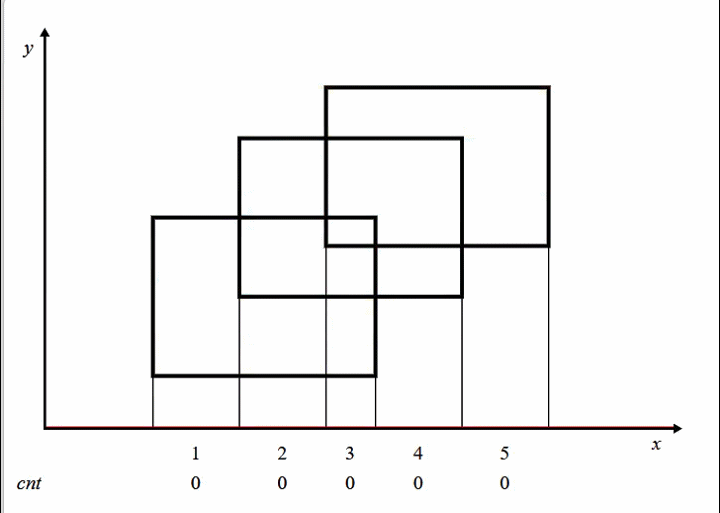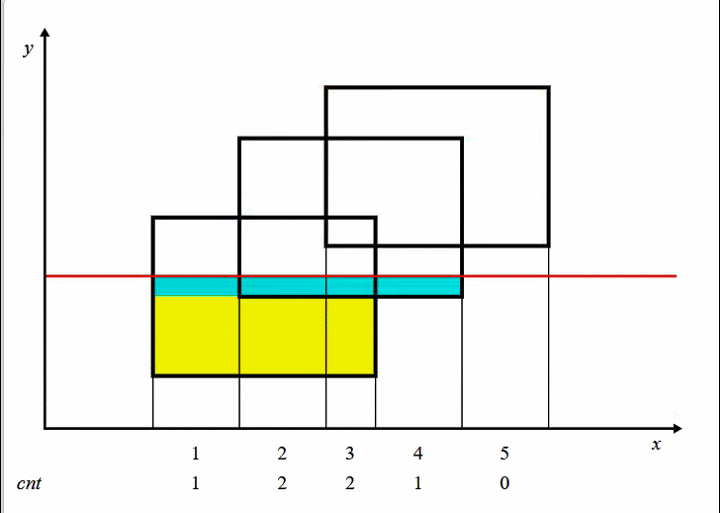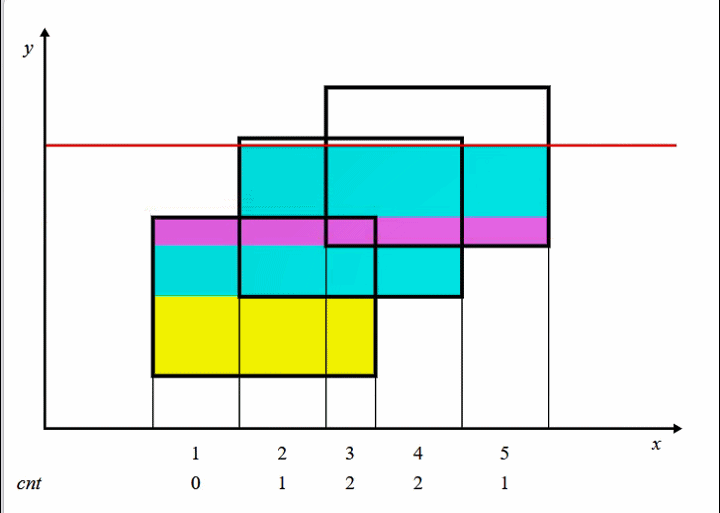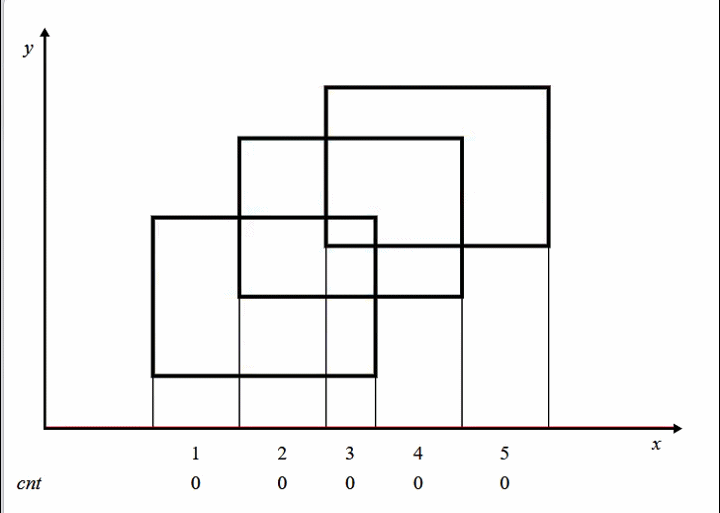
![2023年6月上海月赛甲组T3 方格计数题解]() 2023年6月上海月赛甲组T3 方格计数题解 题目大意有一个 $n$行、$m$列的方格,每个格子上可以写 $0$ 或 $1$两种数字,一开始每个格子上都写着数字 $1$。小爱会进行 $k$ 轮反转操作,每轮游戏他会选择一块区域,左上角为$(x_1, y_1)$,右下角为 $(x_2, y_2)$,并将该区域内所有的数字反转(即原来为 $1$ 的反转为 $0$ ,原来为 $0$ 的反转为 $1$) 。请问, $k$ 轮过后,整个方格中仍为 $1$ 的方格的数量。数据范围$ 1 \le k \le 10^5 $$1 \le n,m,x_i,y_i \le 10^9$算法思路本题采用扫描线算法,扫描线需要使用一种叫做线段树的数据结构。为了更好的理解本题和阅读的连贯性,引用OI-WIKI关于扫描线算法的部分内容。引入 Atlantis 问题在二维坐标系上,给出多个矩形的左下以及右上坐标,求出所有矩形构成的图形的面积。根据图片可知总面积可以直接暴力即可求出面积,如果数据大了怎么办?这时就需要讲到扫描线算法。现在假设我们有一根线,从下往上开始扫描:如图所示,我们可以把整个矩形分成如图各个颜色不同的小矩形,那么这个小矩形的高就是我们扫过的距离,那么剩下了一个变量,那就是矩形的长一直在变化。我们的线段树就是为了维护矩形的长,我们给每一个矩形的上下边进行标记,下面的边标记为 1,上面的边标记为 -1,每遇到一个矩形时,我们知道了标记为 1 的边,我们就加进来这一条矩形的长,等到扫描到 -1 时,证明这一条边需要删除,就删去,利用 1 和 -1 可以轻松的到这种状态。还要注意这里的线段树维护的并不是线段的一个端点,而指的是一段区间。根据数据范围可能需要进行离散化或动态开点。本题与Atlantis区别Atlantis是计算面积而本题是计算方格数量,计算方法类似,但方格数量与线段长度在处理上还是有些区别的。Atlantis一段区间可以被多个矩形覆盖,被一个矩形覆盖和多个矩形覆盖效果一样。但方格计数不同,覆盖奇数次等于覆盖一次,偶数次等于没有覆盖。这个规律提示我们可以使用异或,奇偶性来完成题目。分享一下,我自己解决这两个问题方法。时间上并非最优,上海月赛测$400ms$左右,但很好理解。首先,把格子横坐标离散化。离散化后,若有$M$个不同的 $x$ 坐标值,分别对应原始值$raw(1),raw(2),raw(3),...,raw(M)$。扫描线至多被分成$M-1$段,其中第 $i \space (1\le i \le M-1)$ 段为区间$[raw(i),raw(i+1))$或$[raw(i),raw(i+1)-1]$。左闭右开我们不会重复统计端点的格子,且 $i$ 区间内部有$raw(i+1) - raw(i)$个方格。建立数组 $t$ ,用$t[i]$ 记录第 $i$ 段格子上写 $0$ 的格子数量,当然后面我们需用线段树维护 $t[i]$ 。若离散化后,某次更新$x_1=3 ,x_2=5$,需要更新区间 $3$ 与区间 $4$。$x_2$ 这个位置方格还有没计数啊。这个问题思考了一段时间。我们可再建立数组 $w$,用 $w[x]$ 记录离散化后 $x$ 这个点被操作次数。线段树同时利用数组 $t$ 和 $w$ 就可以计算出闭区间写 $0$ 的格子的数量。void changeSeg(int p, int l, int r, int x) { if (l <= t[p].l && t[p].r <= r) { t[p].add += x;//加标记 t[p].len = a[t[p].r+1] - a[t[p].l] - t[p].len;//0,1数量互换 return; } spread(p); int mid = (t[p].l+t[p].r)>>1; if (l <= mid) changeSeg(p<<1, l, r, x); if (mid < r) changeSeg(p<<1|1, l, r, x); t[p].len = t[p<<1].len+t[p<<1|1].len; }void changePoint(int p,int l,int r,int x){ if (l <= t[p].l && t[p].r <= r) {//包含这个端点的区间根据w[l]数值进行更新 if((t[p].add + w[l] + x) & 1) t[p].len++; else t[p].len--; w[l] += x; return; } spread(p); int mid = (t[p].l+t[p].r)>>1; if (l <= mid) changePoint(p<<1, l, r, x); if (mid < r) changePoint(p<<1|1, l, r, x); t[p].len = t[p<<1].len+t[p<<1|1].len; } 注意这两个函数很像,为了节约代码行数可以合并成为一个函数,但会导致思路不清晰。for (int i = 1; i < k; ++i) { int l = query(e[i].x1),r = query(e[i].x2); if(r > l) changeSeg(1, l, r-1, e[i].k);//区间更新 changePoint(1, r, r, e[i].k);//单点更新 if(e[i+1].y != e[i].y){ ans += 1ll * t[1].len * (e[i+1].y - e[i].y); } }总体来说就是更新两次,先更新线段树维护区间,再更新端点,这样可确保不多不少的统计。若 $l,r$ 相等则只进行单点更新即可。{dotted startColor="#ff6c6c" endColor="#1989fa"/}更新一下,一直以来对changePoint不顺眼,再想能不能只保留一个changeSeg。如果只保留changeSeg函数,那必须让changeSeg函数可以处理单点更新。猛然发现,上述区间更新方法保持不变,一个点也是可以构成区间,只需让起点不变,终点加一,这样更新时$x2 > x1$。举例若离散化后,某次更新$x_1=3 ,x_2=4$。需要更新区间为$3$,涉及格子数量为$[raw(3),raw(4)-1]$,假设此时是单点更新,那么$raw(4)$就会恰好比$raw(3)$大$1$,就是更新$[raw(3),raw(3)]$这个点。for (int i = 1; i <= k; ++i) { int x1, y1, x2, y2; scanf("%d%d%d%d",&x1,&y1,&x2,&y2); e[(i<<1)-1] = (edge){y1, x1, x2+1, 1}; e[i<<1] = (edge){y2+1, x1, x2+1, -1}; //加入线段 a[(i<<1)-1] = x1, a[i<<1] = x2+1; }如此时间会更加优秀~~
2023年6月上海月赛甲组T3 方格计数题解 题目大意有一个 $n$行、$m$列的方格,每个格子上可以写 $0$ 或 $1$两种数字,一开始每个格子上都写着数字 $1$。小爱会进行 $k$ 轮反转操作,每轮游戏他会选择一块区域,左上角为$(x_1, y_1)$,右下角为 $(x_2, y_2)$,并将该区域内所有的数字反转(即原来为 $1$ 的反转为 $0$ ,原来为 $0$ 的反转为 $1$) 。请问, $k$ 轮过后,整个方格中仍为 $1$ 的方格的数量。数据范围$ 1 \le k \le 10^5 $$1 \le n,m,x_i,y_i \le 10^9$算法思路本题采用扫描线算法,扫描线需要使用一种叫做线段树的数据结构。为了更好的理解本题和阅读的连贯性,引用OI-WIKI关于扫描线算法的部分内容。引入 Atlantis 问题在二维坐标系上,给出多个矩形的左下以及右上坐标,求出所有矩形构成的图形的面积。根据图片可知总面积可以直接暴力即可求出面积,如果数据大了怎么办?这时就需要讲到扫描线算法。现在假设我们有一根线,从下往上开始扫描:如图所示,我们可以把整个矩形分成如图各个颜色不同的小矩形,那么这个小矩形的高就是我们扫过的距离,那么剩下了一个变量,那就是矩形的长一直在变化。我们的线段树就是为了维护矩形的长,我们给每一个矩形的上下边进行标记,下面的边标记为 1,上面的边标记为 -1,每遇到一个矩形时,我们知道了标记为 1 的边,我们就加进来这一条矩形的长,等到扫描到 -1 时,证明这一条边需要删除,就删去,利用 1 和 -1 可以轻松的到这种状态。还要注意这里的线段树维护的并不是线段的一个端点,而指的是一段区间。根据数据范围可能需要进行离散化或动态开点。本题与Atlantis区别Atlantis是计算面积而本题是计算方格数量,计算方法类似,但方格数量与线段长度在处理上还是有些区别的。Atlantis一段区间可以被多个矩形覆盖,被一个矩形覆盖和多个矩形覆盖效果一样。但方格计数不同,覆盖奇数次等于覆盖一次,偶数次等于没有覆盖。这个规律提示我们可以使用异或,奇偶性来完成题目。分享一下,我自己解决这两个问题方法。时间上并非最优,上海月赛测$400ms$左右,但很好理解。首先,把格子横坐标离散化。离散化后,若有$M$个不同的 $x$ 坐标值,分别对应原始值$raw(1),raw(2),raw(3),...,raw(M)$。扫描线至多被分成$M-1$段,其中第 $i \space (1\le i \le M-1)$ 段为区间$[raw(i),raw(i+1))$或$[raw(i),raw(i+1)-1]$。左闭右开我们不会重复统计端点的格子,且 $i$ 区间内部有$raw(i+1) - raw(i)$个方格。建立数组 $t$ ,用$t[i]$ 记录第 $i$ 段格子上写 $0$ 的格子数量,当然后面我们需用线段树维护 $t[i]$ 。若离散化后,某次更新$x_1=3 ,x_2=5$,需要更新区间 $3$ 与区间 $4$。$x_2$ 这个位置方格还有没计数啊。这个问题思考了一段时间。我们可再建立数组 $w$,用 $w[x]$ 记录离散化后 $x$ 这个点被操作次数。线段树同时利用数组 $t$ 和 $w$ 就可以计算出闭区间写 $0$ 的格子的数量。void changeSeg(int p, int l, int r, int x) { if (l <= t[p].l && t[p].r <= r) { t[p].add += x;//加标记 t[p].len = a[t[p].r+1] - a[t[p].l] - t[p].len;//0,1数量互换 return; } spread(p); int mid = (t[p].l+t[p].r)>>1; if (l <= mid) changeSeg(p<<1, l, r, x); if (mid < r) changeSeg(p<<1|1, l, r, x); t[p].len = t[p<<1].len+t[p<<1|1].len; }void changePoint(int p,int l,int r,int x){ if (l <= t[p].l && t[p].r <= r) {//包含这个端点的区间根据w[l]数值进行更新 if((t[p].add + w[l] + x) & 1) t[p].len++; else t[p].len--; w[l] += x; return; } spread(p); int mid = (t[p].l+t[p].r)>>1; if (l <= mid) changePoint(p<<1, l, r, x); if (mid < r) changePoint(p<<1|1, l, r, x); t[p].len = t[p<<1].len+t[p<<1|1].len; } 注意这两个函数很像,为了节约代码行数可以合并成为一个函数,但会导致思路不清晰。for (int i = 1; i < k; ++i) { int l = query(e[i].x1),r = query(e[i].x2); if(r > l) changeSeg(1, l, r-1, e[i].k);//区间更新 changePoint(1, r, r, e[i].k);//单点更新 if(e[i+1].y != e[i].y){ ans += 1ll * t[1].len * (e[i+1].y - e[i].y); } }总体来说就是更新两次,先更新线段树维护区间,再更新端点,这样可确保不多不少的统计。若 $l,r$ 相等则只进行单点更新即可。{dotted startColor="#ff6c6c" endColor="#1989fa"/}更新一下,一直以来对changePoint不顺眼,再想能不能只保留一个changeSeg。如果只保留changeSeg函数,那必须让changeSeg函数可以处理单点更新。猛然发现,上述区间更新方法保持不变,一个点也是可以构成区间,只需让起点不变,终点加一,这样更新时$x2 > x1$。举例若离散化后,某次更新$x_1=3 ,x_2=4$。需要更新区间为$3$,涉及格子数量为$[raw(3),raw(4)-1]$,假设此时是单点更新,那么$raw(4)$就会恰好比$raw(3)$大$1$,就是更新$[raw(3),raw(3)]$这个点。for (int i = 1; i <= k; ++i) { int x1, y1, x2, y2; scanf("%d%d%d%d",&x1,&y1,&x2,&y2); e[(i<<1)-1] = (edge){y1, x1, x2+1, 1}; e[i<<1] = (edge){y2+1, x1, x2+1, -1}; //加入线段 a[(i<<1)-1] = x1, a[i<<1] = x2+1; }如此时间会更加优秀~~ -
![2023年7月上海月赛甲组T3最长上升子序列(二)题解]() 2023年7月上海月赛甲组T3最长上升子序列(二)题解 题目大意有 $n$ 个空白方格从左到右排成一行,编号以此为$1..n$。小爱可以给每个格子填上一个数字,其中对于编号为 $i$ 的格子,可以填入的数字的范围为给定的 $[l_i,r_i]$。现在,小爱想知道,如何选择合适的填法,才能使填入后这 $n$ 个数字组成的序列 $a_1,a_2,a_3,...,a_n$ 的最长上升子序列上度最长,本题只需输出最长长度即可。数据范围$1 \le n \le 10^5 , 1 \le l_i \le r_i \le 10^9$算法思路可以想到这是一个变种的最长上升子序列$dp$问题,由于数据范围较大,定是需要思考$O(nlogn)$算法,但不妨碍我们从简单思路出发来探究问题。我先用普通最长上升序列算法来设计$dp$状态, $dp[k]$ 长度为$k$的最长上升子序列的结尾的填入数字的最小值。对于变种最长上升子序列问题,也很容易想到$dp$数组是单调递增的,构建长度更长的序列,一定也需要更大的结尾数字。假设从前$i-1$号格子已经就算出了一段$dp$数组,$curMax$为当前计算出的最后一项的下标,注意下标也代表这最大上升长度。考虑第$i$格子时,有如下几种情况:$l_i > dp[curMax]$,则$dp[curMax+1] = l_i$。$l_i == dp[curMax]$ 且 $l_i < r_i$,则$dp[curMax+1] = l_i + 1$。$l_i == dp[curMax]$ 且 $l_i == r_i$, 则无需更新。在$dp$数组中找到大于 $l_i$ 最小位置 $x$,找到小于 $r_i$ 的最大位置 $y$。 若$x <= y$, 则 $i$ 格子加入使得 $[x,y]$ 区间内最长上升序列长度都加一,且最小结尾数字只需加一即可。做法上我们使区间内所有数字加一,并向后平移一个位置。平移之后,x位置会有空缺。若$l_i > dp[x-1]$, $dp[x] = li$, 否则 $dp[x] = l_i + 1$。若$x > y$,则说明 $l_i$ 只能更新位置 $x$ 的最小结尾数字若$l_i > dp[x-1]$ , $dp[x] = l_i$ ,否则若$r_i > l_i$,$dp[x] = l_i+1$ 。由于$dp$数组是单调的所以$x$ 和 $y$ 位置都可以二分拿到。唯一头疼是第$4$种情况下,区间更新和平移数组非常耗时。有没有一种数据结构,可以动态插入数据到指定位置,相当于平移指定位置后面的数据,且能够对指定区间元素实现统一的操作呢?平衡树(带区间操作)有,不过我们需要手写平衡树。可能你也听过一些平衡树,比如红黑树,树堆Treap,伸展树Splay等等吧。在这里推荐新手们,学一学FHQTreap,范浩强大神提出的一种无旋转Treap,性能不差,而且很容易实现区间操作,代码非常好写。区间操作非常类似线段树打懒标记和标记下传。通过平衡树我们把上述所有情况都可以$O(logn)$,算法的总体复杂度就是$O(nlogn)$。对于FHQTreap讲解 推荐参考一下这篇文章。
2023年7月上海月赛甲组T3最长上升子序列(二)题解 题目大意有 $n$ 个空白方格从左到右排成一行,编号以此为$1..n$。小爱可以给每个格子填上一个数字,其中对于编号为 $i$ 的格子,可以填入的数字的范围为给定的 $[l_i,r_i]$。现在,小爱想知道,如何选择合适的填法,才能使填入后这 $n$ 个数字组成的序列 $a_1,a_2,a_3,...,a_n$ 的最长上升子序列上度最长,本题只需输出最长长度即可。数据范围$1 \le n \le 10^5 , 1 \le l_i \le r_i \le 10^9$算法思路可以想到这是一个变种的最长上升子序列$dp$问题,由于数据范围较大,定是需要思考$O(nlogn)$算法,但不妨碍我们从简单思路出发来探究问题。我先用普通最长上升序列算法来设计$dp$状态, $dp[k]$ 长度为$k$的最长上升子序列的结尾的填入数字的最小值。对于变种最长上升子序列问题,也很容易想到$dp$数组是单调递增的,构建长度更长的序列,一定也需要更大的结尾数字。假设从前$i-1$号格子已经就算出了一段$dp$数组,$curMax$为当前计算出的最后一项的下标,注意下标也代表这最大上升长度。考虑第$i$格子时,有如下几种情况:$l_i > dp[curMax]$,则$dp[curMax+1] = l_i$。$l_i == dp[curMax]$ 且 $l_i < r_i$,则$dp[curMax+1] = l_i + 1$。$l_i == dp[curMax]$ 且 $l_i == r_i$, 则无需更新。在$dp$数组中找到大于 $l_i$ 最小位置 $x$,找到小于 $r_i$ 的最大位置 $y$。 若$x <= y$, 则 $i$ 格子加入使得 $[x,y]$ 区间内最长上升序列长度都加一,且最小结尾数字只需加一即可。做法上我们使区间内所有数字加一,并向后平移一个位置。平移之后,x位置会有空缺。若$l_i > dp[x-1]$, $dp[x] = li$, 否则 $dp[x] = l_i + 1$。若$x > y$,则说明 $l_i$ 只能更新位置 $x$ 的最小结尾数字若$l_i > dp[x-1]$ , $dp[x] = l_i$ ,否则若$r_i > l_i$,$dp[x] = l_i+1$ 。由于$dp$数组是单调的所以$x$ 和 $y$ 位置都可以二分拿到。唯一头疼是第$4$种情况下,区间更新和平移数组非常耗时。有没有一种数据结构,可以动态插入数据到指定位置,相当于平移指定位置后面的数据,且能够对指定区间元素实现统一的操作呢?平衡树(带区间操作)有,不过我们需要手写平衡树。可能你也听过一些平衡树,比如红黑树,树堆Treap,伸展树Splay等等吧。在这里推荐新手们,学一学FHQTreap,范浩强大神提出的一种无旋转Treap,性能不差,而且很容易实现区间操作,代码非常好写。区间操作非常类似线段树打懒标记和标记下传。通过平衡树我们把上述所有情况都可以$O(logn)$,算法的总体复杂度就是$O(nlogn)$。对于FHQTreap讲解 推荐参考一下这篇文章。 -
![2023年5月上海月赛甲组T1子集和(六)题解]() 2023年5月上海月赛甲组T1子集和(六)题解 题目描述给定一个长度为 n 的序列 $a_1,a_2,a_3,...,a_n$ 与一个参数 $k$ 。 现有 $q$ 次询问,每次询问一个区间$[L,R]$,请你求出该区间内所有子集和中,有多少个子集和恰好是 $k$ 的倍数,答案对$998244353$取模。(注意:所有子集中包含空集)算法思路本题采用优雅的暴力结构——分块。预处理将序列分成$M=\sqrt{n}$块,每块分别记录三类数据$lr[M][M][20],rr[M][M][20],br[M][20]$。$lr[i][j][r]$表示第$i$块,从块内倒数第$1$个数到正数第$j$个数所有组合中余数为$r$的个数,共$M$个块,每块需要$O(Mk)$,合计$O(nk)$。$rr[i][j][r]$表示第$i$块,从块内正数第$1$个数到正数第$j$个数所有组合中余数为$r$的个数,共$M$个块,每块需要$O(Mk)$,合计$O(nk)$。$br[i][r]$表示第$i$块,从头至尾所有组合中余数为$r$的个数,可以复用$rr[i][M][r]$。注意根据乘法原理,例如余数2的个数*余数3的个数就是增加的余数5的个数。 我们可以$O(k^2)$来合并两个区间。为了加快查询速度,我们再预处理一类数据$ss[M][M][20]$,$ss[i][j][r]$表示从第i块到第j块所有组合中余数为$r$的个数。在求解 $ss[i][j]$ 时我们可以利用$ss[i][j-1]$ 和$br[j]$ 合并来得到,共有$M^2$块需要合并。至此,我们预处理完毕,预处理时间复杂度$O(nk + nk^2)$。查询查询可以分三类。若$l,r$在同一块内,则直接暴力计算即可,$O(Mk)$。若分散$l,r$分散在两个相邻的块,假设 $l$ 在 $i$ 块,第 $s$ 个位置,$r$ 在 $j$ 块第 $t$ 个位置,直接$O(k)$快速合并$lr[i][s]$与$rr[j][t]$记录的余数个数信息,最终答案只需统计余数为0个数,故$O(k)$。$l,r$相距较远。同样假设 $l$ 在 $i$ 块,第 $s$ 个位置, $r$ 在 $j$ 块第 $t$ 个位置。现合并$lr[i][s]$与$rr[j][t]$记录的余数个数信息$O(k^2)$,再将合并结果与$ss[i+1][j-1]$记录的余数个数信息合并$O(k)$。对于查询来说,第3类查询数量最多,因此单次查询复杂度可认定为$O(k^2)$。总体时间复杂度$O(nk^2+qk^2)$即$O((n+q)k^2)$类似数据结构 猫树猫树,一种改版线段树。思想和我的这种分块方式类似,所以我管我搞出来的这个分块叫做猫块。
2023年5月上海月赛甲组T1子集和(六)题解 题目描述给定一个长度为 n 的序列 $a_1,a_2,a_3,...,a_n$ 与一个参数 $k$ 。 现有 $q$ 次询问,每次询问一个区间$[L,R]$,请你求出该区间内所有子集和中,有多少个子集和恰好是 $k$ 的倍数,答案对$998244353$取模。(注意:所有子集中包含空集)算法思路本题采用优雅的暴力结构——分块。预处理将序列分成$M=\sqrt{n}$块,每块分别记录三类数据$lr[M][M][20],rr[M][M][20],br[M][20]$。$lr[i][j][r]$表示第$i$块,从块内倒数第$1$个数到正数第$j$个数所有组合中余数为$r$的个数,共$M$个块,每块需要$O(Mk)$,合计$O(nk)$。$rr[i][j][r]$表示第$i$块,从块内正数第$1$个数到正数第$j$个数所有组合中余数为$r$的个数,共$M$个块,每块需要$O(Mk)$,合计$O(nk)$。$br[i][r]$表示第$i$块,从头至尾所有组合中余数为$r$的个数,可以复用$rr[i][M][r]$。注意根据乘法原理,例如余数2的个数*余数3的个数就是增加的余数5的个数。 我们可以$O(k^2)$来合并两个区间。为了加快查询速度,我们再预处理一类数据$ss[M][M][20]$,$ss[i][j][r]$表示从第i块到第j块所有组合中余数为$r$的个数。在求解 $ss[i][j]$ 时我们可以利用$ss[i][j-1]$ 和$br[j]$ 合并来得到,共有$M^2$块需要合并。至此,我们预处理完毕,预处理时间复杂度$O(nk + nk^2)$。查询查询可以分三类。若$l,r$在同一块内,则直接暴力计算即可,$O(Mk)$。若分散$l,r$分散在两个相邻的块,假设 $l$ 在 $i$ 块,第 $s$ 个位置,$r$ 在 $j$ 块第 $t$ 个位置,直接$O(k)$快速合并$lr[i][s]$与$rr[j][t]$记录的余数个数信息,最终答案只需统计余数为0个数,故$O(k)$。$l,r$相距较远。同样假设 $l$ 在 $i$ 块,第 $s$ 个位置, $r$ 在 $j$ 块第 $t$ 个位置。现合并$lr[i][s]$与$rr[j][t]$记录的余数个数信息$O(k^2)$,再将合并结果与$ss[i+1][j-1]$记录的余数个数信息合并$O(k)$。对于查询来说,第3类查询数量最多,因此单次查询复杂度可认定为$O(k^2)$。总体时间复杂度$O(nk^2+qk^2)$即$O((n+q)k^2)$类似数据结构 猫树猫树,一种改版线段树。思想和我的这种分块方式类似,所以我管我搞出来的这个分块叫做猫块。